modeling with distance functions

'Graphic Study'에서 DEV여우 작성 함

원문링크


Unity Graphic Programing 보다가..

primitives

All primitives are centered at the origin. You will have to transform the point to get arbitrarily rotated, translated and scaled objects (see below).


Sphere - signed - exact

float sdSphere( vec3 p, float s )
{
  return length(p)-s;
}

Box - unsigned - exact

float udBox( vec3 p, vec3 b )
{
  return length(max(abs(p)-b,0.0));
}

Round Box - unsigned - exact

float udRoundBox( vec3 p, vec3 b, float r )
{
  return length(max(abs(p)-b,0.0))-r;
}

Box - signed - exact

float sdBox( vec3 p, vec3 b )
{
  vec3 d = abs(p) - b;
  return min(max(d.x,max(d.y,d.z)),0.0) + length(max(d,0.0));
}

Torus - signed - exact

float sdTorus( vec3 p, vec2 t )
{
  vec2 q = vec2(length(p.xz)-t.x,p.y);
  return length(q)-t.y;
}

Cylinder - signed - exact

float sdCylinder( vec3 p, vec3 c )
{
  return length(p.xz-c.xy)-c.z;
}

Cone - signed - exact

float sdCone( vec3 p, vec2 c )
{
    // c must be normalized
    float q = length(p.xy);
    return dot(c,vec2(q,p.z));
}

Plane - signed - exact

float sdPlane( vec3 p, vec4 n )
{
  // n must be normalized
  return dot(p,n.xyz) + n.w;
}

Hexagonal Prism - signed - exact

float sdHexPrism( vec3 p, vec2 h )
{
    vec3 q = abs(p);
    return max(q.z-h.y,max((q.x*0.866025+q.y*0.5),q.y)-h.x);
}

Triangular Prism - signed - exact

float sdTriPrism( vec3 p, vec2 h )
{
    vec3 q = abs(p);
    return max(q.z-h.y,max(q.x*0.866025+p.y*0.5,-p.y)-h.x*0.5);
}

Capsule / Line - signed - exact

float sdCapsule( vec3 p, vec3 a, vec3 b, float r )
{
    vec3 pa = p - a, ba = b - a;
    float h = clamp( dot(pa,ba)/dot(ba,ba), 0.0, 1.0 );
    return length( pa - ba*h ) - r;
}

Capped cylinder - signed - exact

float sdCappedCylinder( vec3 p, vec2 h )
{
  vec2 d = abs(vec2(length(p.xz),p.y)) - h;
  return min(max(d.x,d.y),0.0) + length(max(d,0.0));
}

Capped Cone - signed - bound

float sdCappedCone( in vec3 p, in vec3 c )
{
    vec2 q = vec2( length(p.xz), p.y );
    vec2 v = vec2( c.z*c.y/c.x, -c.z );
    vec2 w = v - q;
    vec2 vv = vec2( dot(v,v), v.x*v.x );
    vec2 qv = vec2( dot(v,w), v.x*w.x );
    vec2 d = max(qv,0.0)*qv/vv;
    return sqrt( dot(w,w) - max(d.x,d.y) ) * sign(max(q.y*v.x-q.x*v.y,w.y));
}

Ellipsoid - signed - bound

float sdEllipsoid( in vec3 p, in vec3 r )
{
    return (length( p/r ) - 1.0) * min(min(r.x,r.y),r.z);
}

Triangle - unsigned - exact

float dot2( in vec3 v ) { return dot(v,v); }
float udTriangle( vec3 p, vec3 a, vec3 b, vec3 c )
{
    vec3 ba = b - a; vec3 pa = p - a;
    vec3 cb = c - b; vec3 pb = p - b;
    vec3 ac = a - c; vec3 pc = p - c;
    vec3 nor = cross( ba, ac );

    return sqrt(
    (sign(dot(cross(ba,nor),pa)) +
     sign(dot(cross(cb,nor),pb)) +
     sign(dot(cross(ac,nor),pc))<2.0)
     ?
     min( min(
     dot2(ba*clamp(dot(ba,pa)/dot2(ba),0.0,1.0)-pa),
     dot2(cb*clamp(dot(cb,pb)/dot2(cb),0.0,1.0)-pb) ),
     dot2(ac*clamp(dot(ac,pc)/dot2(ac),0.0,1.0)-pc) )
     :
     dot(nor,pa)*dot(nor,pa)/dot2(nor) );
}

Quad - unsigned - exact

float dot2( in vec3 v ) { return dot(v,v); }
float udQuad( vec3 p, vec3 a, vec3 b, vec3 c, vec3 d )
{
    vec3 ba = b - a; vec3 pa = p - a;
    vec3 cb = c - b; vec3 pb = p - b;
    vec3 dc = d - c; vec3 pc = p - c;
    vec3 ad = a - d; vec3 pd = p - d;
    vec3 nor = cross( ba, ad );

    return sqrt(
    (sign(dot(cross(ba,nor),pa)) +
     sign(dot(cross(cb,nor),pb)) +
     sign(dot(cross(dc,nor),pc)) +
     sign(dot(cross(ad,nor),pd))<3.0)
     ?
     min( min( min(
     dot2(ba*clamp(dot(ba,pa)/dot2(ba),0.0,1.0)-pa),
     dot2(cb*clamp(dot(cb,pb)/dot2(cb),0.0,1.0)-pb) ),
     dot2(dc*clamp(dot(dc,pc)/dot2(dc),0.0,1.0)-pc) ),
     dot2(ad*clamp(dot(ad,pd)/dot2(ad),0.0,1.0)-pd) )
     :
     dot(nor,pa)*dot(nor,pa)/dot2(nor) );
}


Most of these functions can be modified to use other norms than the euclidean. By replacing length(p), which computes (x^2+y^2+z^2)^(1/2) by (x^n+y^n+z^n)^(1/n) one can get variations of the basic primitives that have rounded edges rather than sharp ones.


Torus82 - signed

float sdTorus82( vec3 p, vec2 t )
{
  vec2 q = vec2(length2(p.xz)-t.x,p.y);
  return length8(q)-t.y;
}

Torus88 - signed

float sdTorus88( vec3 p, vec2 t )
{
  vec2 q = vec2(length8(p.xz)-t.x,p.y);
  return length8(q)-t.y;
}



distance operations

The d1 and d2 parameters in the following functions are the distance to the two distance fields to combine together.


Union

float opU( float d1, float d2 )
{
    return min(d1,d2);
}

Substraction

float opS( float d1, float d2 )
{
    return max(-d1,d2);
}

Intersection

float opI( float d1, float d2 )
{
    return max(d1,d2);
}



domain operations

Where "primitive", in the examples below, is any distance formula really (one of the basic primitives above, a combination, or a complex distance field).


Repetition

float opRep( vec3 p, vec3 c )
{
    vec3 q = mod(p,c)-0.5*c;
    return primitve( q );
}

Rotation/Translation

vec3 opTx( vec3 p, mat4 m )
{
    vec3 q = invert(m)*p;
    return primitive(q);
}

Scale

float opScale( vec3 p, float s )
{
    return primitive(p/s)*s;
}



distance deformations

You must be carefull when using distance transformation functions, as the field created might not be a real distance function anymore. You will probably need to decrease your step size, if you are using a raymarcher to sample this. The displacement example below is using sin(20*p.x)*sin(20*p.y)*sin(20*p.z) as displacement pattern, but you can of course use anything you might imagine. As for smin() function in opBlend(), please read the smooth minimum article in this same site. 


Displacement

float opDisplace( vec3 p )
{
    float d1 = primitive(p);
    float d2 = displacement(p);
    return d1+d2;
}

Blend

float opBlend( vec3 p )
{
    float d1 = primitiveA(p);
    float d2 = primitiveB(p);
    return smin( d1, d2 );
}



domain deformations

Domain deformation functions do not preserve distances neither. You must decrease your marching step to properly sample these functions (proportionally to the maximun derivative of the domain distortion function). Of course, any distortion function can be used, from twists, bends, to random noise driven deformations.


Twist

float opTwist( vec3 p )
{
    float c = cos(20.0*p.y);
    float s = sin(20.0*p.y);
    mat2  m = mat2(c,-s,s,c);
    vec3  q = vec3(m*p.xz,p.y);
    return primitive(q);
}

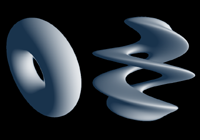Cheap Bend

float opCheapBend( vec3 p )
{
    float c = cos(20.0*p.y);
    float s = sin(20.0*p.y);
    mat2  m = mat2(c,-s,s,c);
    vec3  q = vec3(m*p.xy,p.z);
    return primitive(q);
}


A reference implementation of most of these primitives and operators can be found here (click in the image to rotate the camera, or in the title to jump to the source code):




저작자표시 비영리 변경금지

'Graphic Study' 카테고리의 다른 글

GDC 2011 – Approximating Translucency for a Fast, Cheap and Convincing Subsurface Scattering Look  (0) 2018.05.31
Advance in Real-Time Rendering - SIGGRAPH 2017  (0) 2018.05.30
Quick And Easy GPU Random Numbers In D3D11  (0) 2018.05.15
ASTC Format에 대해  (0) 2018.03.23
The Book of Shaders  (0) 2018.03.18
  1. 아직 등록된 댓글이 없습니다.

Habradol Advanced shaders in Unity

'Unity Shaders'에서 DEV여우 작성 함

Habradol.com Link



저작자표시 비영리 변경금지
  1. 아직 등록된 댓글이 없습니다.

Unity 2018.1 Release

'Engine News (Unreal & Unity)'에서 DEV여우 작성 함

Link1


Link2(Blog)




CtrlCV 포기..




저작자표시 비영리 변경금지

'Engine News (Unreal & Unity)' 카테고리의 다른 글

Unity at GDC Keynote - March 19, 2018  (0) 2018.03.23
Epic Games Releases $12 Million Worth of Paragon Assets for Free  (0) 2018.03.20
Unreal 4.19 Release  (0) 2018.03.18
  1. 아직 등록된 댓글이 없습니다.
<<이전 글 1 ··· 7 8 9 10 11 12 13 ··· 23 다음 글>>

티스토리툴바